В этой статье мы рассмотрим ключевые аспекты создания ретро фотографий и как они могут
Выбор напольного покрытия в квартире, где есть маленькие дети, требует особого внимания. Необходимо учитывать
Толщина рукоятки также имеет значение. Ножи для филе, которые не требуют много работы, имеют
Когда под рукой ничего не подходит, можно промыть водкой мелкие ранки и принимать ее
Слои необходимо хорошо утрамбовать. После этих этапов на укрепляющий слой выстилается песчаная подушка, для
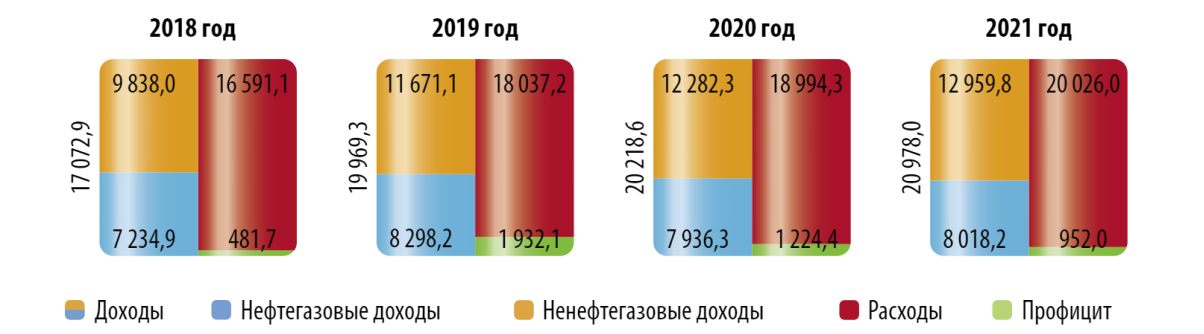
Сброс пароля или смена привязанного почтового ящика блокирует Торговую площадку на пять дней (или
Вариантов как получить скины множество, а вот как продать все скины кс го выгодно
Эта статья будет полезна и начинающим, и продвинутым художникам. Вы получите проверенные советы, которые
Качественные столы с регулировкой высоты и дополнительными функциями, повышающими комфорт. Критерии выбора столов с
Рейтинг лучших производителей японских подгузников по мнению экспертов и отзывам покупателей.
Анализируем репутацию бренда,
Крем под подгузник - ТЕСТ. Я проанализировала состав кремов под подгузник известных брендов, чтобы
Топ-10 лучших спальных мешков (коконов и одеял) для туризма и кемпинга. Подборка лучших спальников
Комплексно-тематический план. Ситуация «Пришли морозные деньки, достали лыжи и коньки» (подготовительная группа)
Какой шлем лучше выбрать для горных лыж? Обзор отдельных моделей и критерии выбора.
Точилка для ножей является неотъемлемым атрибутом каждой кухни. Благодаря ее использованию кухонный нож будет
Рейтинг лучших подводок-фломастеров по мнению экспертов и отзывам покупателей. Независимое расследование лучших производителей:
Artdeco, L'Oreal,
Когда речь заходит о эффективном ежедневном ношении всего необходимого EDC-снаряжения, на ум сразу же
Виды рюкзаков, в которых удобно и безопасно переносить ноутбук. Преимущества и рейтинг качественных моделей.
Наборы для первоклассников это очень полезное и удобное приобретение. Ведь в таком наборе есть
Выбираем колыбель-кроватку для новорожденного: виды люлек, критерии выбора, плюсы и минусы
Рейтинг растущих парт: описание моделей и их характеристики. Достоинства и недостатки такого типа парт,
🎁 Что можно подарить подростку на Новый год? Полезные и оригинальные подарки, техника и
ТОП самых новых идей что нужно подарить ребенку на 2 года, чтобы он развивался
Выбирая, что подарить ребенку 10, 11, 12, 13 лет на Новый год 2022, воспользуйтесь
Оборудование кабинета ИЗО школы - перечень, оснащение, материал, оформление, ФГОС.
Прочитав статью, читатель узнает о том, как выбрать цифровое пианино, каких ошибок стоит избегать
Аккордеон, баян, гармонь: внешние отличия, особенности конструкции и звучания, история инструментов. Виды аккордеонов, особенности
⭐⭐⭐ТОП-10 лучших моделей в категории Акустические системы BEHRINGER. Акустические системы бренда BEHRINGER – рейтинг